

The denominator of the first derivative is equal to zero at \( x = 2\) and therefore \( x = 2 \) is a critical point. Step - 2: Find the critical points (see definition above) of the derivative

Step 3: Evaluate \( f \) at all endpoints and critical points and take the smallest (minimum) and largest (maximum) values.įind the absolute maximum and minimum of function \( f \) defined by \( f(x) = - x^2 + 2 x -2 \ \ \text \) Step 2: Find the critical points of function \( f \) Step 1: Find the first derivative of function \( f \)
#MAX AND MIN CALCULATOR HOW TO#
Note that although there is a local minimum and a local maximum, they are not absolute minimum and maximum.Įxamples with Detailed Solutions How to find absolute minimum and absolute maximum of a function \( f \): In the example below, \( f(x) = x^3 - 2x^2 \) for \( -1\le x \le 5/2 \) where \( -1 \) and \( 5/2 \) are the endpoints of the interval \( \) defining the domain of the function.
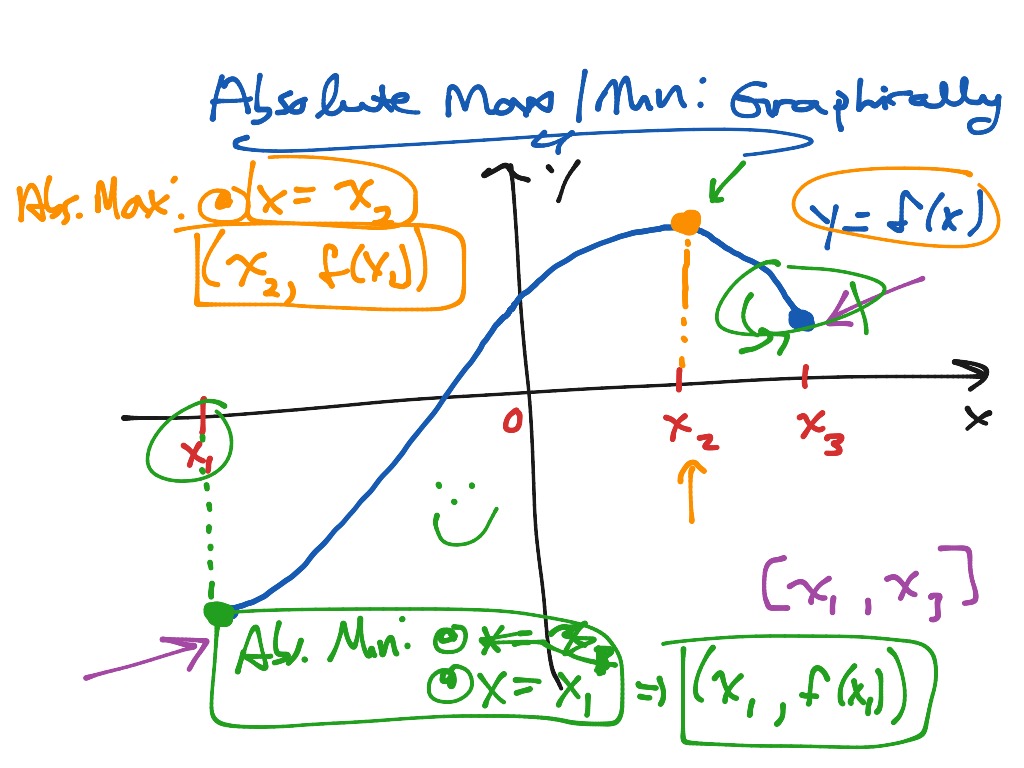
The absolute minimum and maximum of a function may happen at the endpoints of the interval defining the domain of the function. The absolute minimum and maximum of a function may occur at points where the first derivative is undefined as shown in the graph below.Įxample 3 Absolute minimum and maximum at end points We can see that \( f \) has an absolute minimum at \( x = x_1 \) where \( f'(x) = 0 \) and changes sign from negative to positive and has an absolute maximum at \( x = x_2 \) where \( f'(x_2) = 0 \) changes sign from positive to negative.Įxample 2 Absolute minimum and maximum at points where the first derivative is undefined In the system of coordinates below are shown function \( f \) (blue) and its derivative (red). Local minima and maxima of a function occur at values of \( x = x_0 \) included in the domain of \( f \) Theorem: For a continous function on a closed interval \( \), there always exist values \( x_1 \) and \( x_2\) in \( \) such that \( f(x_1) = m \) is an absolute minimum and \( f(x_2) = M \) is an absolute maximum or \( m \le f(x) \le \ M \) for every \( x \in \).Įxamples on absolute maximum and minimum of functions in different situations are discussed graphically.Įxample 1 Absolute minimum and maximum at stationary pointsĪbsolute minimum and maximum of a function may happen at local minimum and maximum respectively as shown in the graph below. Review of Absolute Minimum and Maximum of a Functionĭefinition: Values of \( x \) in the domain of function \( f \) at which \( f '(x) = 0 \) or \( f '(x) \) is undefined are called critical Graphical solutions to the examples are also presented for deep understanding of the absolute minimum and maximum of a given function. The absolute minimum and maximum of a function are studied using graphs and examples with detailed solutions. resistance R L of lines (overhead lines and cables) at 20 ☌.Absolute Minimum and Maximum of a Function.motors shall be included if appropriate.equivalent impedance Z Q are used to represent external networks, the minimum equivalent short-circuit impedance shall be used.the maximum contribution from power plants and network feeders.voltage factor c max according to Table 1 shall be applied for the calculation of maximum short-circuit currents in the absence of a national standard.When calculating maximum short-circuit currents, the following conditions will be considered: Table 1 Voltage Factor c Nominal voltage U nġ) c maxU n should not exceed the highest voltage Um for equipment of power systems.Ģ) If no nominal voltage is defined c maxU n = U m or c minU n = 0.90 × U m should be applied.ģ) For low-voltage systems with a tolerance of +6 %, for example systems renamed from 380 V to 400 V.Ĥ) For low-voltage systems with a tolerance of +10 %. These assumptions are not strictly true for the power systems, however, the result of the calculations are generally of acceptable accuracy. All line capacitances, shunt admittances and non-rotating loads are neglected.Arc resistances are not taken into account.The impedance of the transformers is referred to the tap-changer in main position.

No change in the type of short circuit involved, that is, a three-phase short circuit remains three-phase and a line-to-earth short circuit remains line-to-earth during the time of short circuit.The calculation of maximum and minimum short-circuit currents as per IEC 60909 is based on the following assumptions.


 0 kommentar(er)
0 kommentar(er)
